PENENTUAN CADANGAN ASURANSI JIWA MULTILIFE DENGAN ASUMSI SEMI MARKOV
DOI:
https://doi.org/10.23887/wms.v8i1.11854Keywords:
cadangan, asumsi semi markov, probabilitas transisi, intensitas transisi, pendekatan prospektifAbstract
Penelitian ini bertujuan untuk mengetahui cadangan dari asuransi jiwa multi life dengan asumsi semi markov. Asumsi semi markov digunakan dalam membuat model yang menggambarkan ketidakbebasan antara sisa usia hidup pasangan suami dan istri. Dengan asumsi semi markov, transisi antar state tidak hanya mempertimbangkan state saat ini pasangan tersebut berada tetapi juga mempertimbangkan waktu yang dihabiskan pasangan tersebut di state tersebut. Berdasarkan probabilitas transisi antar state kemudian ditentukan intensitas transisinya yang dilanjutkan dengan penentuan premi dan kemudian ditentukan cadangan untuk suatu waktu tertentu dengan pendekatan prospektif. Hasil penelitian menunjukkan terdapat ketidakbebasan antara sisa usia hidup suami dan istri dimana pengaruh kematian pasangan pada istri lebih tinggi dari pada suami, besar premi dan cadangan dapat ditentukan melalui rumus
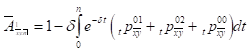
dan
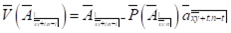
References
Atkinson, K. 1993. Elementary Numerical Analysis Second Edition. John Wiley & Sons. Canada.
Bain, Lee J dan Engelhardt, Max. 1992. Introduction to Probability and Mathematical Statistics. California : Duxbury, 1992
Bowers, N.L., Gerber, H.U., Hickman, J.C., Jones, D.A. dan Nesbitt, C.J., 1997, Actuarial Mathematics 2nd Edition, The Society of Actuaries, Itasca, Illinois.
Hartawan, I G N Yudi. 2013. Pendekatan Model Multi Status Markov Dalam Penentuan Premi Asuransi Jiwa Multi-life. Ejournal undiksha vol 3 no 1: Seminar Nasional FMIPA Undiksha 2013.
Janssen, J., Manca, R., 2006, Applied Semi-Markov Processes, Springer Verlag, New York
Ji, Min., Hardy, Mary. dan Li, Johnny Siu-Hang. 2010. Markoviann Approaches to Joint Life Mortality. North American Actuarial Journal, Volume 15, number 3.
London, Dick, 1997, Survival Models and Their Estimation 3rd Edition, Actex Publication, Winsted
Norberg, R. 1989. Actuarial Analysis of Dependent Lives. Bulletin of the Swiss Association of Actuaries 2: 243–254.
Ross, Sheldon M. 2010. Introduction to Probability Models 10th edition. USA : Elsevier, Inc.
Downloads
Published
Issue
Section
License

Wahana Matematika and Sains is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
